Esta semana vou abordar o seguinte problema do Project Euler.
Consiste em descobrir qual a solução válida mais pequena para o código secreto. Como muitos outros problemas do PE, este pode ser resolvido apenas com papel e lápis.
Vou primeiro explicar esse método e depois estabelecer o paralelo com a programação.
Temos um ficheiro com 50 tentativas de login em que são pedidos certos algarismos da solução (como se fossem coordenadas da matriz bancária), cujo comprimento desconhecemos, mas sempre por ordem. Este é o pormenor que permite resolver o problema.
O primeiro passo é percorrer cada uma das entrada e anotar que números aparecem à direita e esquerda. Se ordenarem o ficheiro e removerem os duplicados terão apenas 33 tentativas para processar.
No final desse passo, deverão ter uma tabela semelhante a esta:
| Esquerda | Número | Direita |
| 1, 2, 3, 6, 7, 8, 9 | 0 | - |
| 3, 7 | 1 | 0, 2, 6, 8, 9 |
| 1, 3, 6, 7 | 2 | 0, 8, 9 |
| 7 | 3 | 0, 1, 2, 6, 8, 9 |
| - | 4 | - |
| - | 5 | - |
| 1, 3, 7 | 6 | 0, 2, 8, 9 |
| - | 7 | 0, 1, 2, 3, 6, 8, 9 |
| 1, 2, 3, 6, 7 | 8 | 0, 9 |
| 1, 2, 3, 6, 7, 8 | 9 | 0 |
Com base nesta tabela, podemos inferir que:
A partir daqui é ir preenchendo os espaços conforme o que a tabela indica quanto aos números à direita e esquerda.
Assim por diante até à solução: 73162890. Não é mais complicado que resolver um Sudoku.
Agora, como podemos validar esta solução utilizando programação?
Consideremos cada elemento do código secreto como sendo um nó de um grafo. A instrução que é pedida (e.g. "3.º, 5.º e 6º algarismos") representa uma sequência de transições.
O que procuramos é então uma ordenação desses nós tal que as restrições existentes (a ordem de apresentação algarismos) sejam cumpridas. Como deduzimos acima que os dígitos serão únicos, sabemos também que o grafo não tem ciclos. Isto porque a ordenação topológica depende do grafo ser a) dirigido; b) acíclico; o chamado DAG - Directed Acyclic Graph.
Outro conceito a reter é que, num grafo, o grau interno corresponde ao número de ligações que chegam e o grau externo é o número de ligações que partem.
O algoritmo que escolhi foi o algoritmo de Khan, provavelmente o mais conhecido.
Uma descrição deste em linguagem corrente é a seguinte (retirada da Wikipedia):
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edge while S is non-empty do remove a node n from S add n to tail of L for each node m with an edge e from n to m do remove edge e from the graph if m has no other incoming edges then insert m into S if graph has edges then return error (graph has at least one cycle) else return L (a topologically sorted order)
Enquanto houver nós com grau interno = 0 (num grafo sem ciclos, o nó inicial cumpre sempre este requisito), adicionamos esse nó n à lista e, de seguida, removemos todas as ligações que partem de n (reduzimos o seu grau externo a zero).
Se no decorrer deste processo algum nó ficar sem ligações (grau interno = 0), esse é adicionado a S e prosseguimos até termos processado todos os arcos ou encontrado um ciclo que nos impede de continuar.
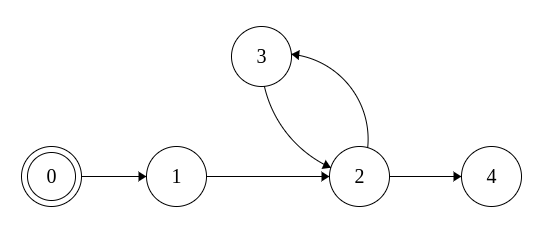
Como podemos ver, é um algoritmo bastante simples, de complexidade O ( |Vértices| + |Arestas| ). Para compreenderem porque o algoritmo falha se tivermos um ciclo, podem executá-lo manualmente neste exemplo:

Implementação exemplo em Python:
def solution():
with open(FILE, 'r') as f:
codes = [ line.strip() for line in f ]
graph = defaultdict(lambda: set()) # Graph as a Dictionary { NODE: [NODES] }
for a, b, c in codes:
graph[a].add(b)
graph[b].add(c)
passcode = list()
digits = {'7'} # We know it starts with 7
while digits: # <=> while not empty
n = digits.pop()
passcode.append(n)
edges = graph.get(n)
if edges is not None:
# Makes a copy
explore = set(edges)
for node in explore:
graph[n].remove(node)
# {y for x in graph.values() for y in x} <=> Every node that is a destination
# values() returns several sets and those are flattened
if node not in {y for x in graph.values() for y in x}:
digits.add(node)
return ''.join(passcode)
No final, obtemos a solução, representando aqui a ordem dos nós no grafo.
Para um problema mais avançado de "encontra a sequência", podem espreitar o PE 185 - Number Mind.
Para mais problemas com grafos, PE 107 - Minimal network, PE 434 - Rigid graphs, PE 81 - Path sum: two ways (82 e 83 também).
Se estiverem interessados em resolver mais problemas do Project Euler, podem adicionar-me lá para trocar ideias. A minha Friend Key é 1064683_5kGuQY3pi0KcVhEm40ypEOPZsSBj0DKX.