Grafos - Ordenação Topológica

A ordenação topológica (em inglês, topological sort) é uma ordenação linear de um dag (direct acyclic graph, i.e., grafo orientado sem ciclos) onde cada nó não aparece antes dos seus antecessores.

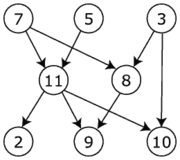
Um exemplo: seja o seguinte dag (ref)

neste caso, existem várias ordenações topológicas possíveis:

• 3, 7, 8, 5, 11, 10, 2, 9
• 5, 7, 3, 8, 11, 10, 9, 2
• 7, 5, 11, 2, 3, 8, 9, 10
• ...

É possível que, num dado problema, exista um critério extra que admite apenas uma ordenação.

Por exemplo, se exigirmos que nós com identificadores menores sejam ordenados primeiro, existe apenas uma solução:

• 3, 5, 7, 8, 11, 2, 9, 10

Um algoritmo

Para devolver uma ordenação topológica genérica (i.e., sem critérios extra) devemos repetir o processo seguinte:

Enquanto houver nós:

1. Encontrar um nó que não tenha antecessores,
2. Juntá-lo à ordenação
3. Removê-lo do grafo (convém trabalhar com uma cópia da estrutura de dados, para não mexermos no original)

A complexidade é dada por O(V+E) sendo V o número de nós e E o número de arestas.

Classe GraphMatrix

Vamos implementar este algoritmo usando os serviços da classe GraphMatrix discutida nos tutoriais anteriores.

Primeiro a função auxiliar seguinte permite encontrar e isolar um nó sem antecessores.

Aqui assumimos que o grafo é sempre um dag:

private boolean[] deactivated;  // vector useful for topSort

// get the index of a node with no in-edges (for topSort)
// returns -1 if no such node found (ie, a cycle exists)
private int getOutNode() {
   int i;
   boolean foundIn=true;

   for(i=0; i<size && foundIn; i++) {
      if (deactivated[i])
         continue;
      foundIn = false;
      for(int j=0; j<size && !foundIn; j++)
         foundIn = weight(j,i) != 0;
   }

   if(!foundIn) {
      isolate(i-1);
      deactivated[i-1] = true;
   }

   return !foundIn ? i-1 : -1; // if all have in-edges, there's a cycle
}

Com este método auxiliar torna-se mais fácil implementar o algoritmo acima.

Cada nó encontrado é colocado uma lista. No fim esta lista é traduzida para um array (que contém os índices dos nós na ordenação topológica).

/**
 * Performs Topological Sort
 * @requires a directed graph
 * @complexity O(V + E)
 * @return an array of indexes with one topological sort of the graph
 *         or null if the graph has cycles (ie, it is not a DAG)
 */
public int[] topSort() {
   ArrayList<Integer> l = new ArrayList<Integer>();
   int node, nodesLeft  = size;
   Graph       cp       = this.copy();
   cp.deactivated       = new boolean[size];

   while(nodesLeft-- > 0) {
      node = cp.getOutNode();  // find & deactivate node with no in-edges
      if (node==-1)
         return null;
      l.add(node);
   }

   return list2array(l);
}

Podem experimentar este novo algoritmo (adicionem estes métodos à classe GraphMatrix) na resolução do problema UVa 200 Rare Order.

Outros problemas que podem ser abordados via ordenação topológica:

• UVa124 - Following Orders (usar backtracking para gerar ordenações válidas)
• UVa872 - Ordering
• UVa10305 - Ordering Tasks
• UVa11686 - Pick up sticks

Uma outra utilidade da ordenação topológica é que serve para verificar se um dado grafo é um DAG, i.e., um Directed Acyclic Graph, um tipo particular de grafo muito usado em aplicações:

/**
 * Checks if graph is a Direct Acyclic Graph
 * @complexity O(V + E)
 * @return true iff graph is DAG
 */
public boolean isDAG() {
   return isDirected==DIRECT && topSort() != null;
}