LISBON

Copyright (c) 2004 Bill Taylor, João Pedro Neto

Lisbon was inspired by Christian Freeling's Havannah.

The game is played on a hexhex board with alternating sizes 8/9 where no edge hex has special status, i.e., corner hexes are not treated differently than any other hexes at the edge. That is achieved by modelling the board perimeter as a circle approximation.

 

Definitions The perimeter consists of all hexes from the board's edges Distances only refer to sizes of paths across the perimeter For any edge hex, the near-opposite hexes are the two farthest edge hexes (which distances are exactly a half-perimeter)

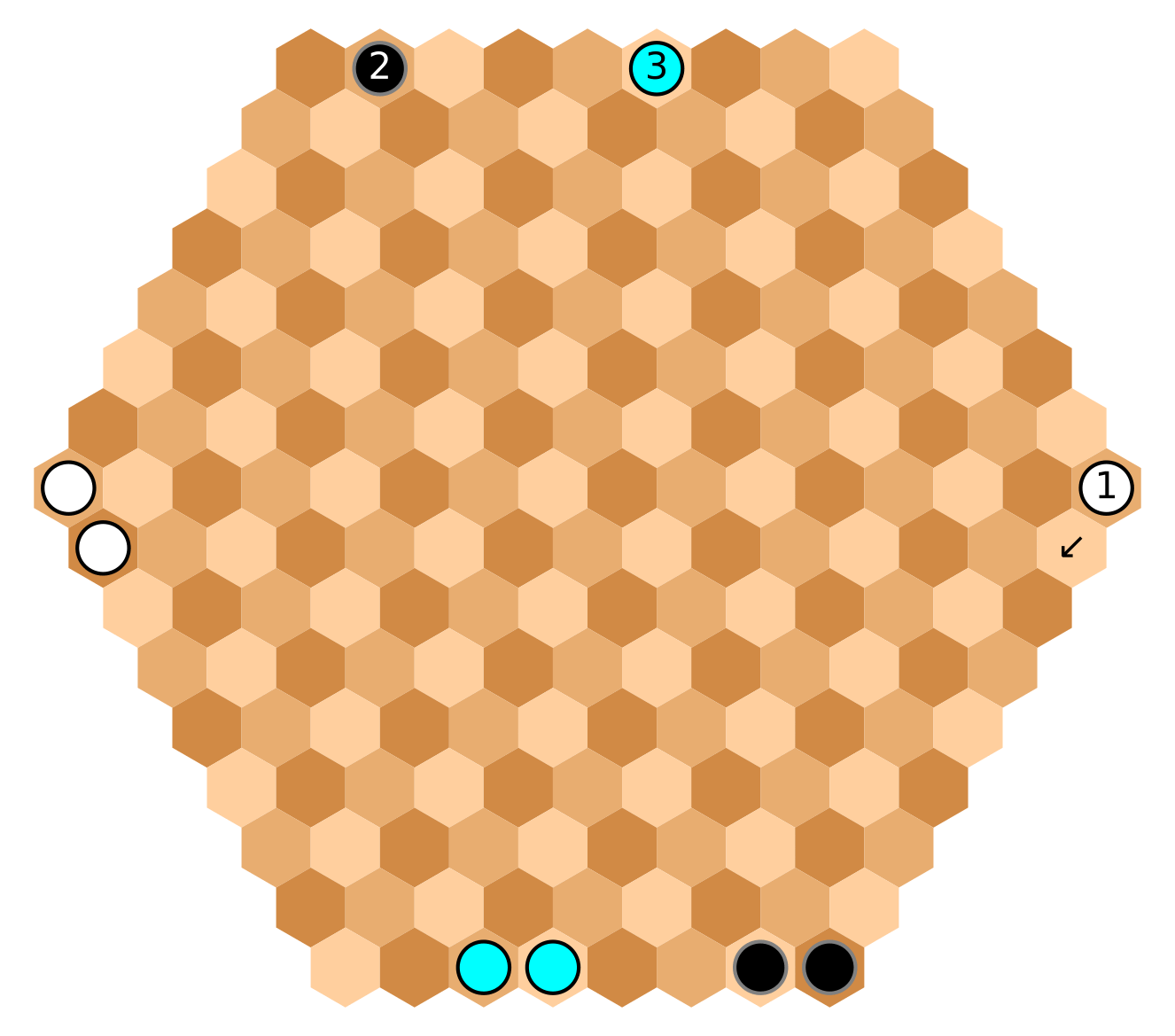
Given this board, for any edge hex, there are always two farthest hexes at distance 21 (half-perimeter). This happens because of the board format, where edges have alternating sizes of eight and nine hexes, resulting in odd-sized half-perimeters.

Here lies a potential problem of lack of clarity: near-opposite stones are not obvious to beginners. But it is a matter of practice. For example, one way to quickly check for near-opposites is starting at a board corner. At a corner, say stone [1], the near-opposites are (a) the other corner, and (b) the other corner's neighbor in the direction of the largest edge (check arrow).

The (counter-)clockwise distance of an edge stone from a corner, like black [2], is the same (counter-)clockwise distance for its near-opposites. Stone [3] is another example, by shifting four edge hexes clockwise.

Rules Players place stones following the progressive sequence 122234445666... No pair of currently placed stones can share the same group Players do not need to use all available moves Winner is whoever makes a connected group of friendly stones that either: includes two near-opposite edge hexes includes three edge hexes, where all the three pair-wise clockwise distances are less than a half-perimeter completely surrounds at least one empty hex or one opponent stone (not includes edges)

The original ruleset used a restricted 12* move sequence. We replaced it with a slow progressive mutator for a faster and more dramatic game. This progressive sequence is less decisive than standard progressive games (where matches end too soon).

Some examples of patterns with three edge hexes:

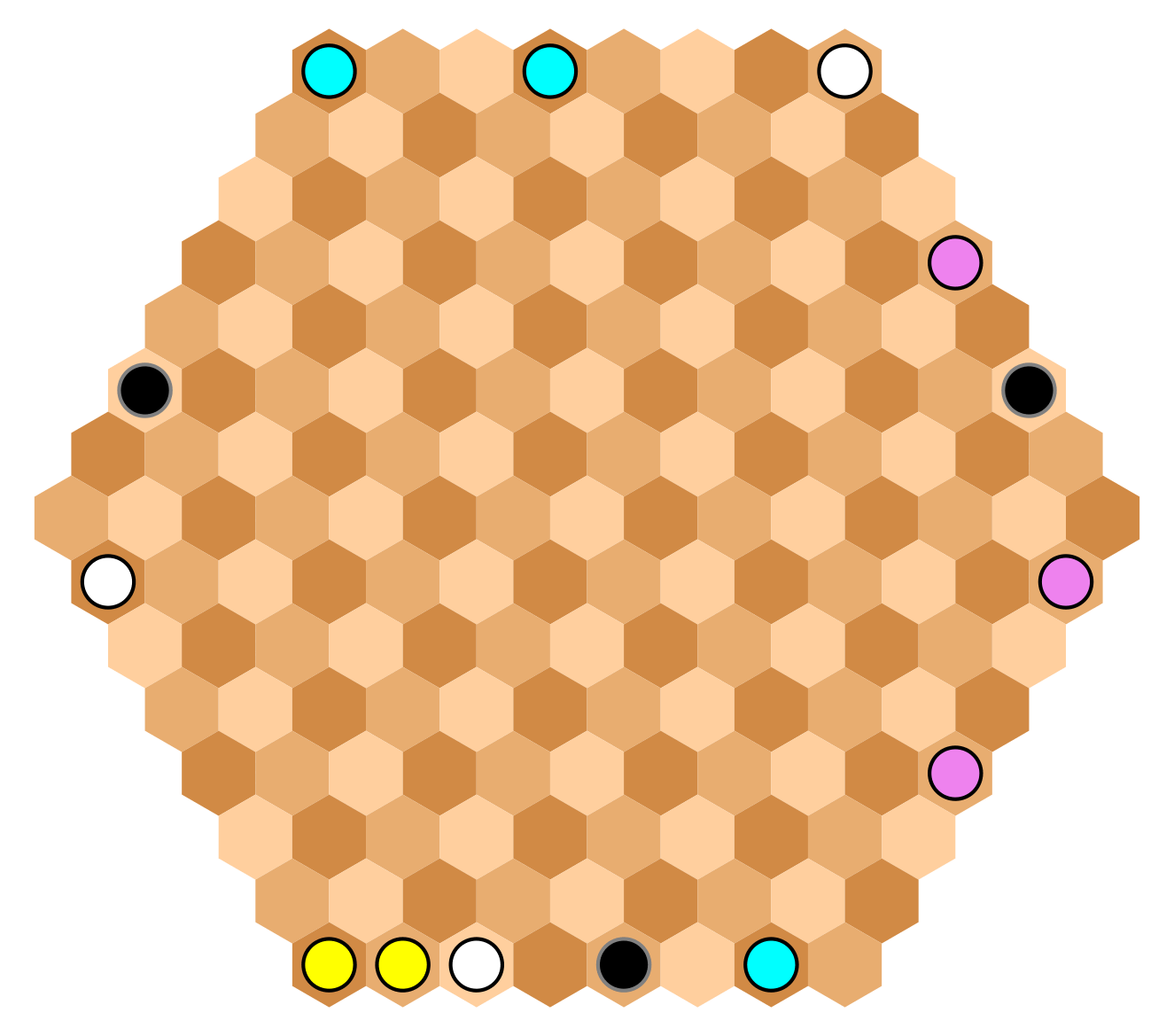
Assume a group connecting the stones of the same color, using only non-edge hexes, in the above diagram:

• The three black stones form a winning pattern; this is an example of a standard Y shape: touching three non-adjacent edges (of course, in Lisbon there is only one edge: the perimeter).

• The three white stones, despite not making a Y, are also a winning pattern, since neither is more than half a distance from the others. Notice that if either one of the lower white stones were where the yellow stones are, that shape would not be winning, given that there would have been a pair of stones with a distance of half the perimeter (it needs to be strictly less than half the perimeter).

• The three cyan stones are also a winning pattern (the upper pair is adjacent to both near-opposites of the lower stone).

• The three purple stones do not form a winning pattern (one pair-wise distance is much greater than a half-perimeter). Notice that if a player has several friendly stones at the edges, to win he needs to select three that make the winning pattern, the remaining unselected stones are immaterial.

The next diagrams show an actual match between us:

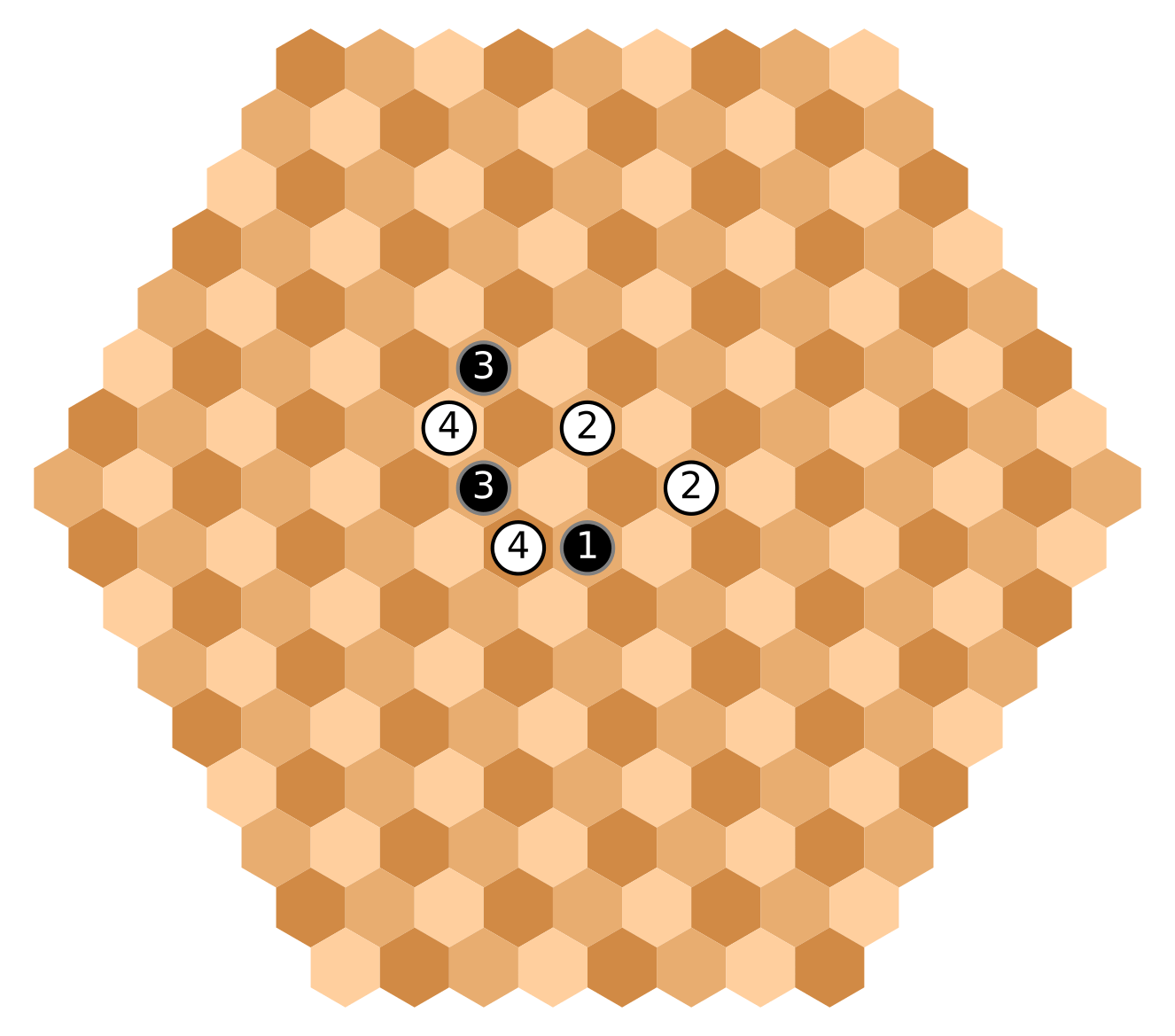
The first four turns with 1,2,2,2 moves. Players are trying to gain the center.
Black cannot cut both [4] to [2] given the group restriction placement rule.

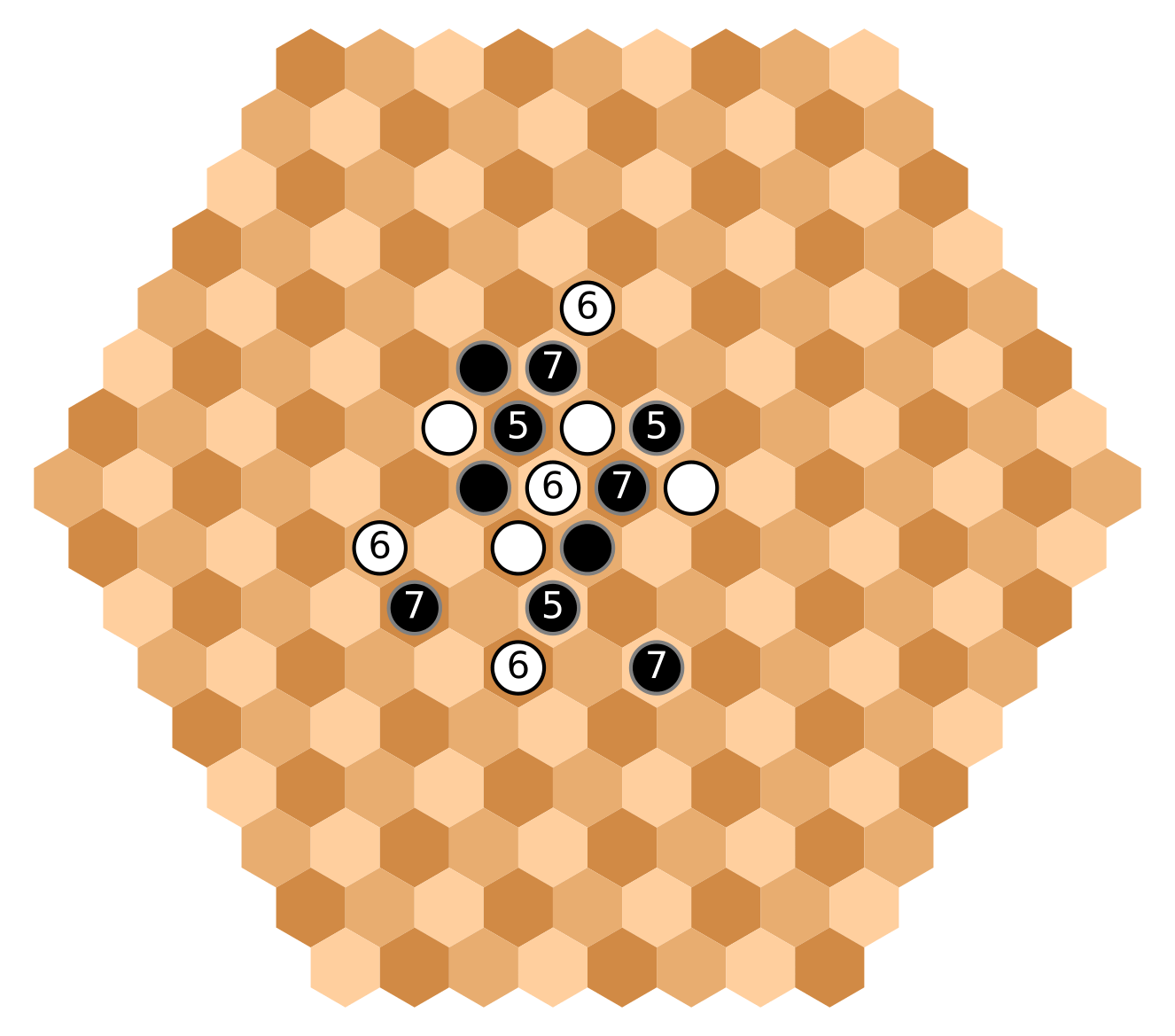
The next three turns. Black is trying to isolate the center white group,
while creating two parallel line groups to reach the edges

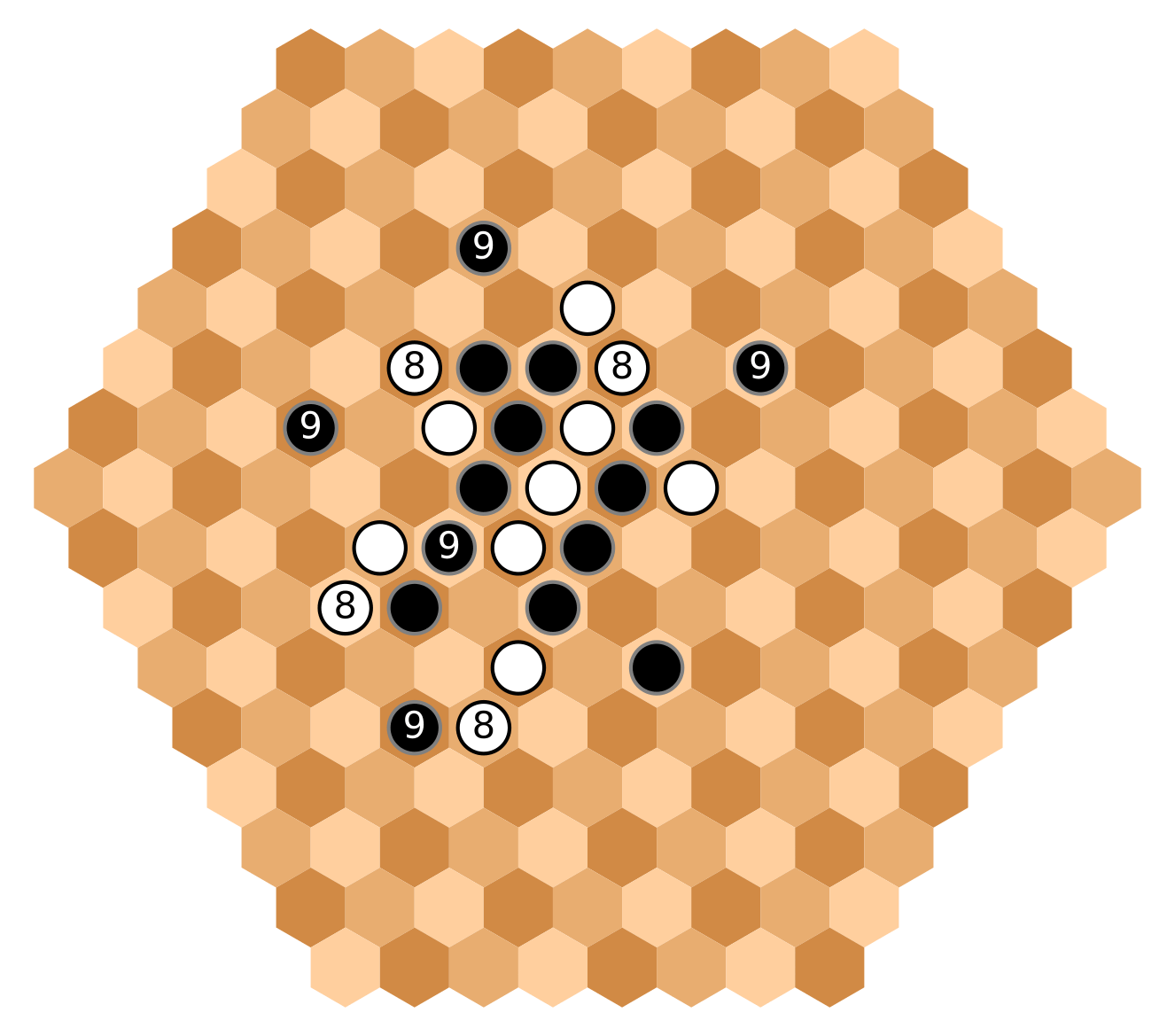
White [8] makes four group extensions, spreading her influence outwards the center.
Three of the five [9] stones, are placed a bit more outside to counter this influence.

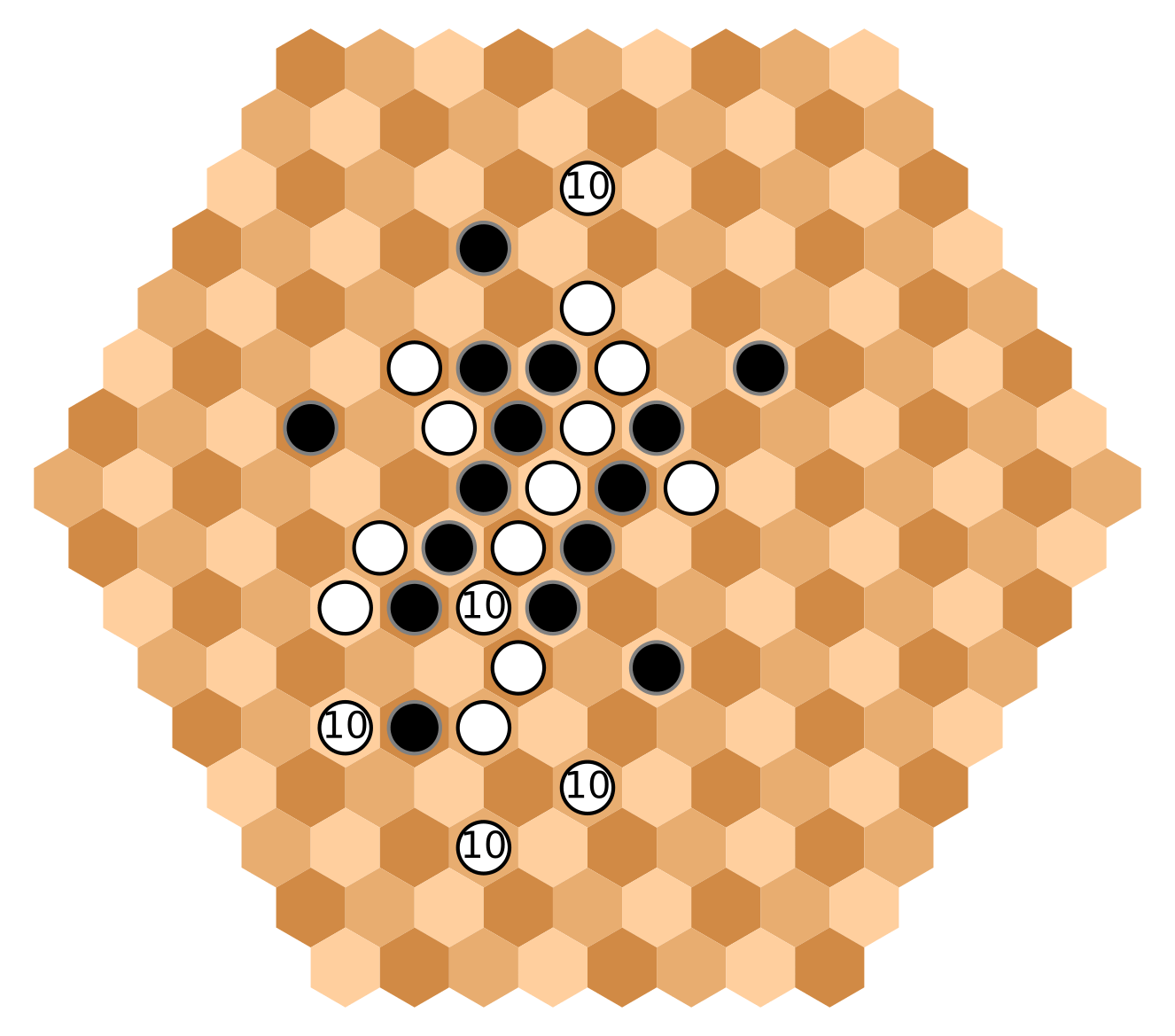
White maintains the integrity of its main group, and spreads to the south perimeter.

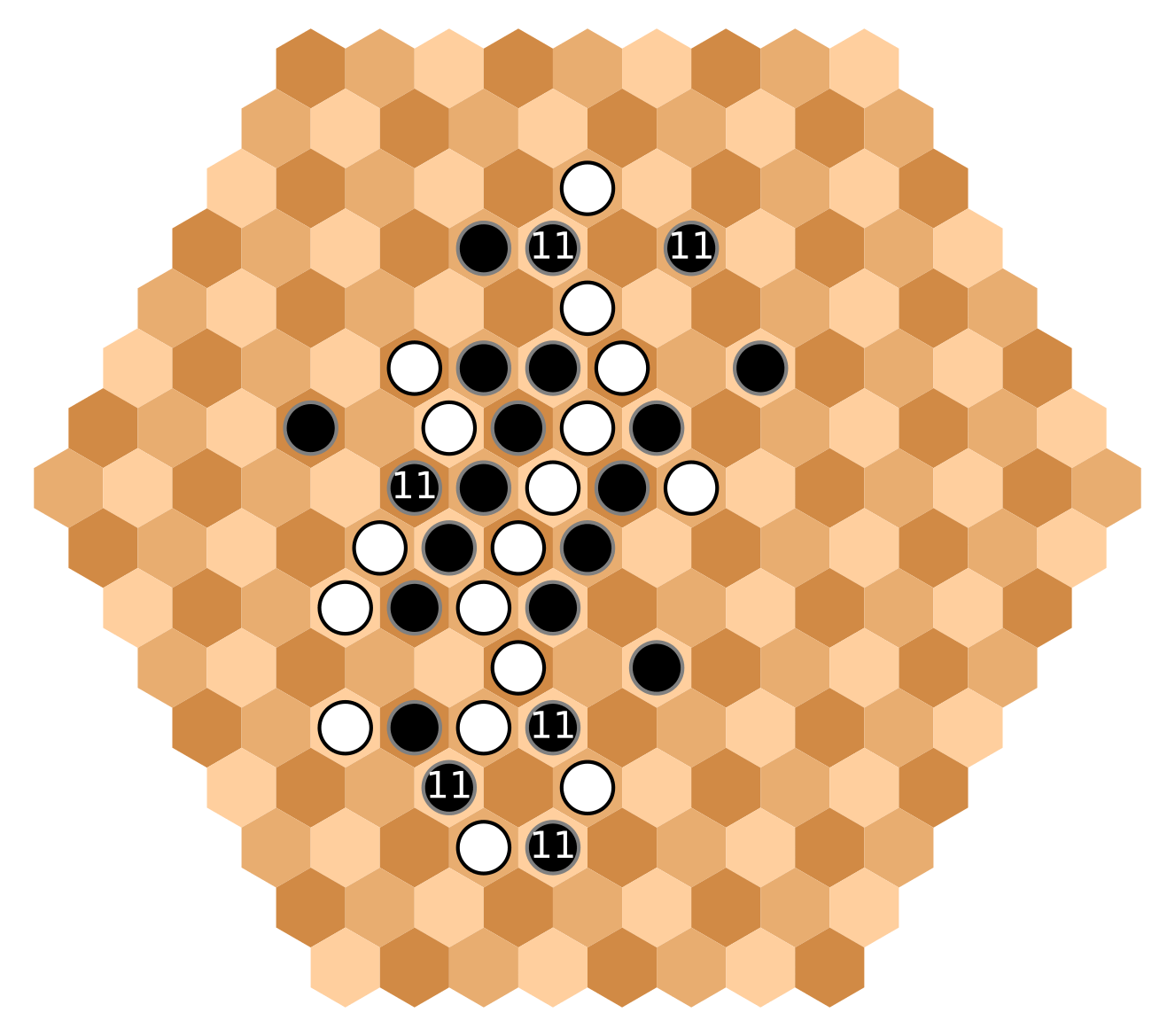
Black is unable to gain the initiative. He uses five or his six moves to try to contain White's vertical expansion.
The single middle stone is trying to keep alive the connection to the western perimeter.

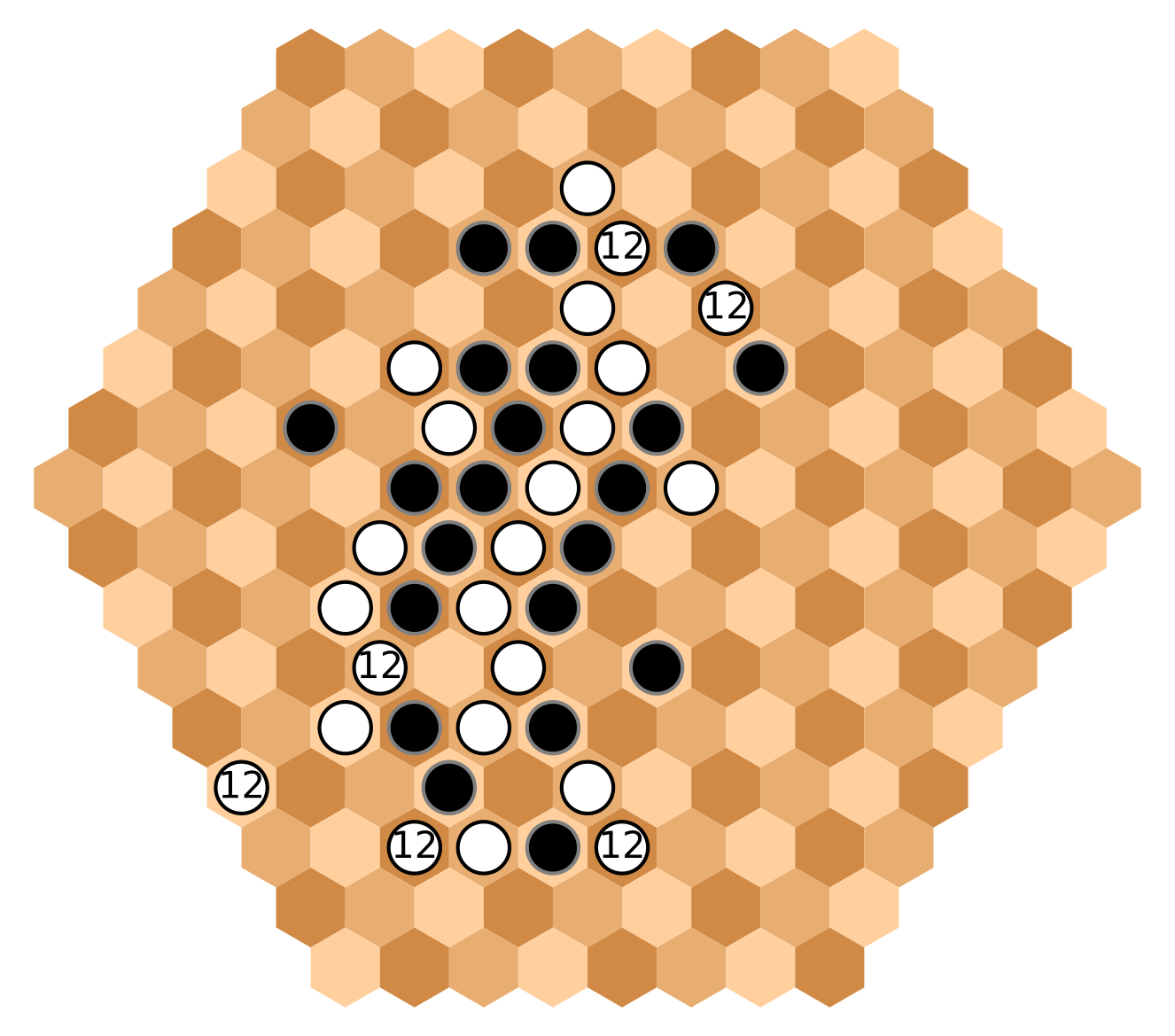
White invests again in the south perimeter, almost guaranteeing its connection.
Notice that Black cannot cut the two white south branches, since they would belong to the same black group.

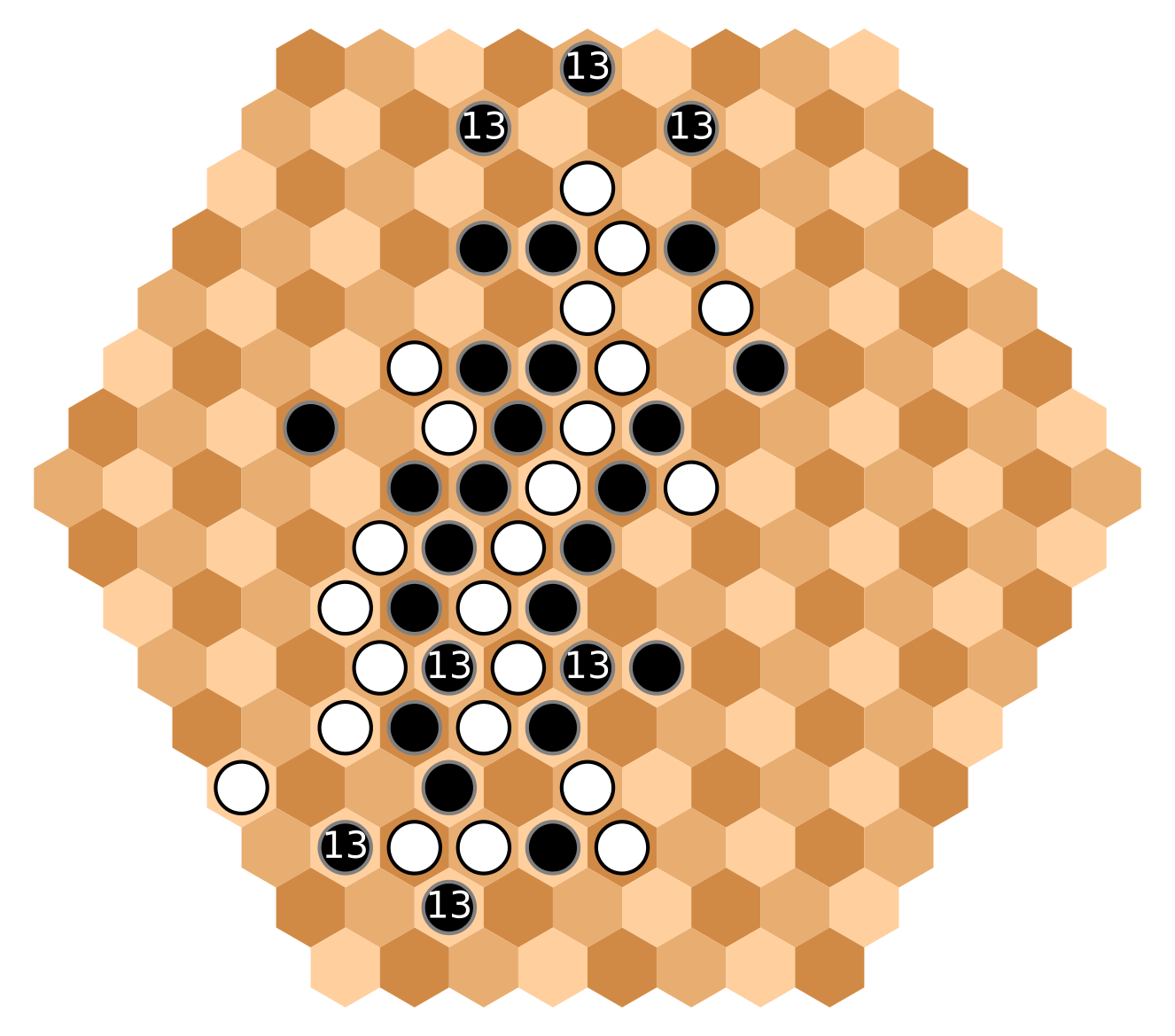
Black tries to build a north wall. In principle this would not be enough to stop
White connecting, but White's central group is very big, and she needs to worry about
the south battle, that might compromise the northern advance.

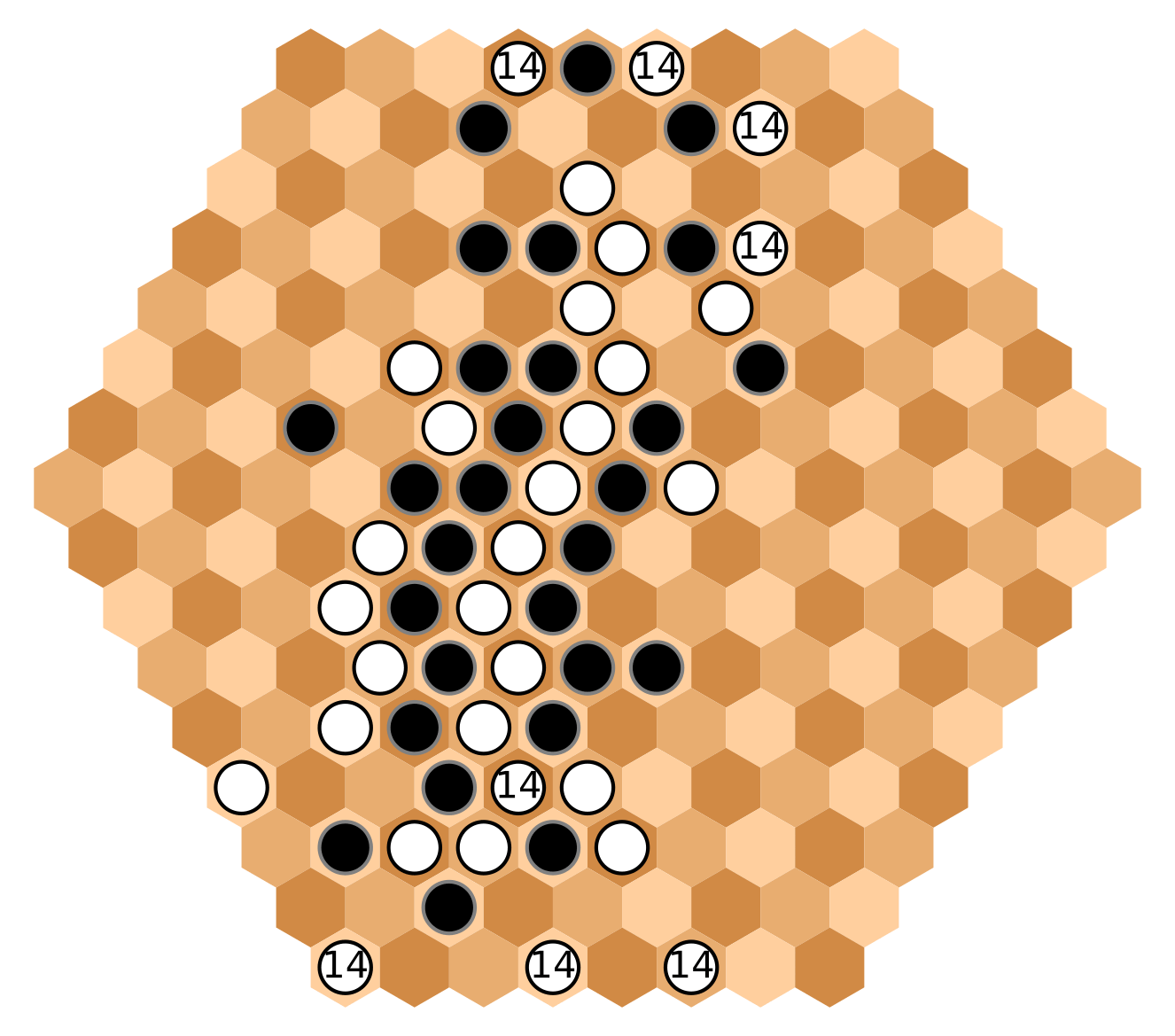
The pace increases. Now we have eight movements per turn. White needs to deviate the
north path, creating a new path to connection, since she needed to connect the central group with
its three south branches/threats. Also, her task is not only to connect opposite edges
("there are no edges") but to connect near-opposite edge hexes.

But now Black has a difficult task, there are multiple connections to cut. It is difficult for him to stop
either the north and the south advances. Still, he tries the following:

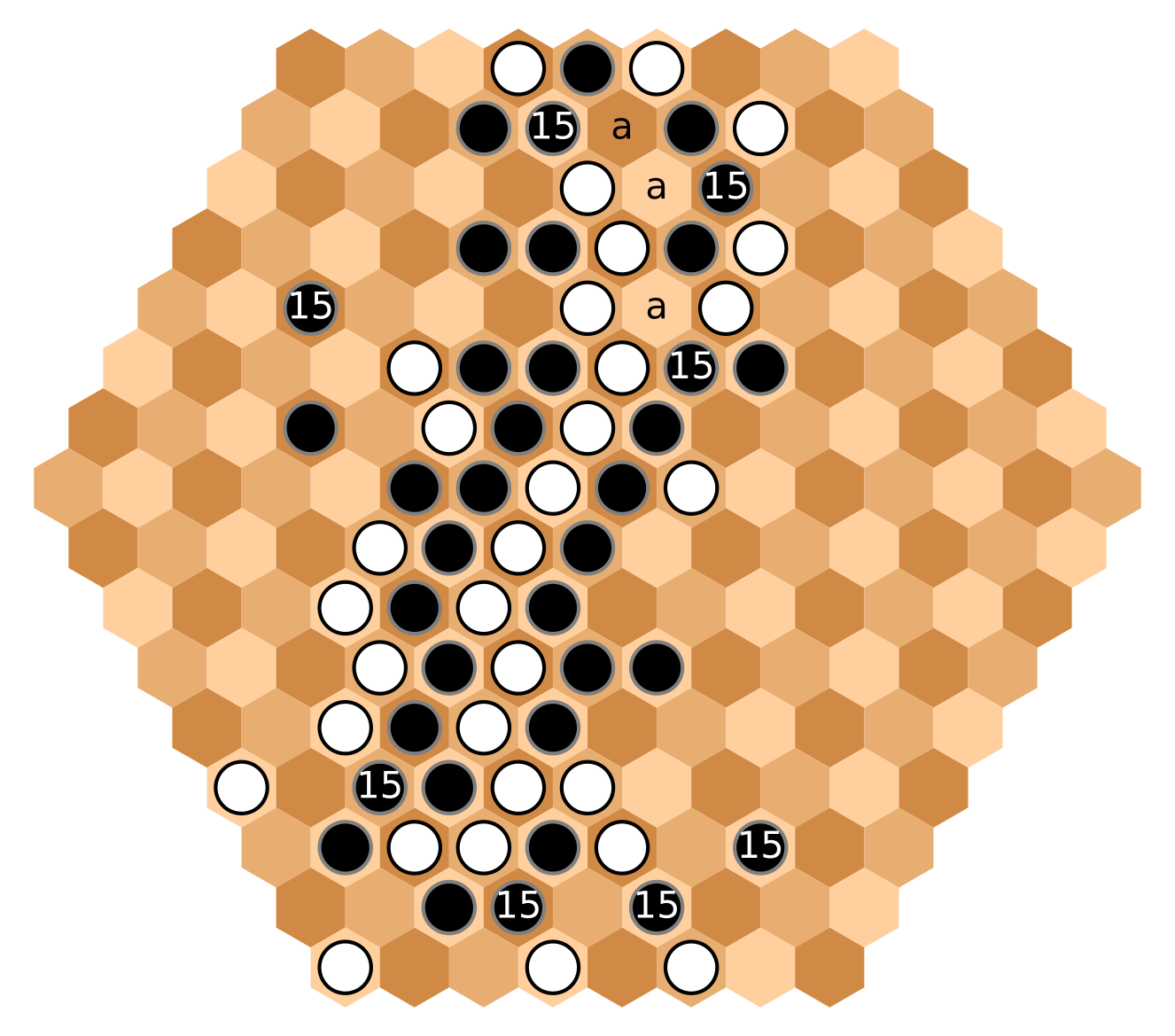
At the south, Black is forcing White to choose a path. No matter the option, this will mean that,
at the north, White will not be able to place stone on the [a] hexes. This gives Black some hope.

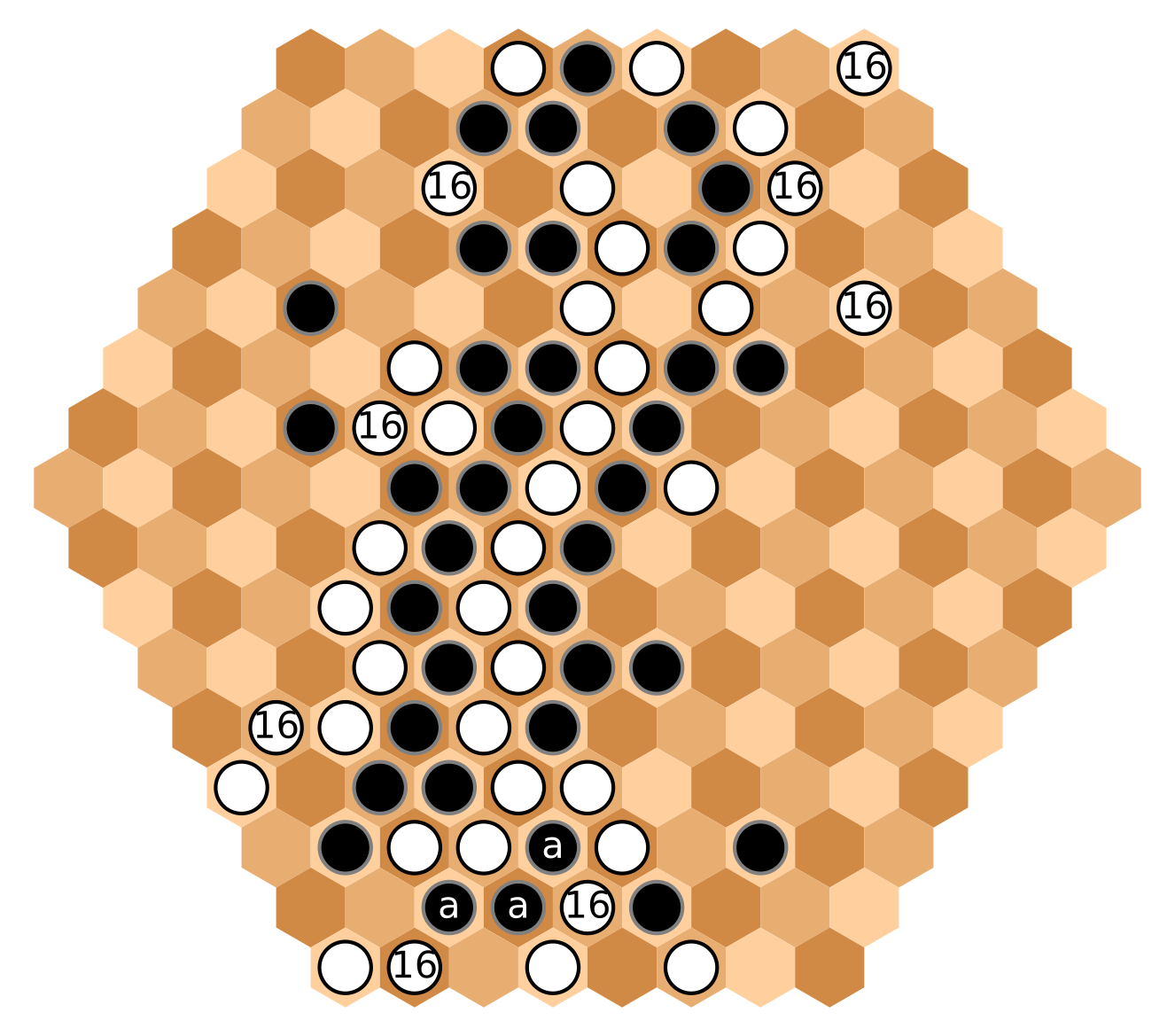
White finally connects to the south perimeter. But to face next turn, she creates alternative routes,
to the southwest and northeast. Also, White is quietly surrounding the three [a] stones.

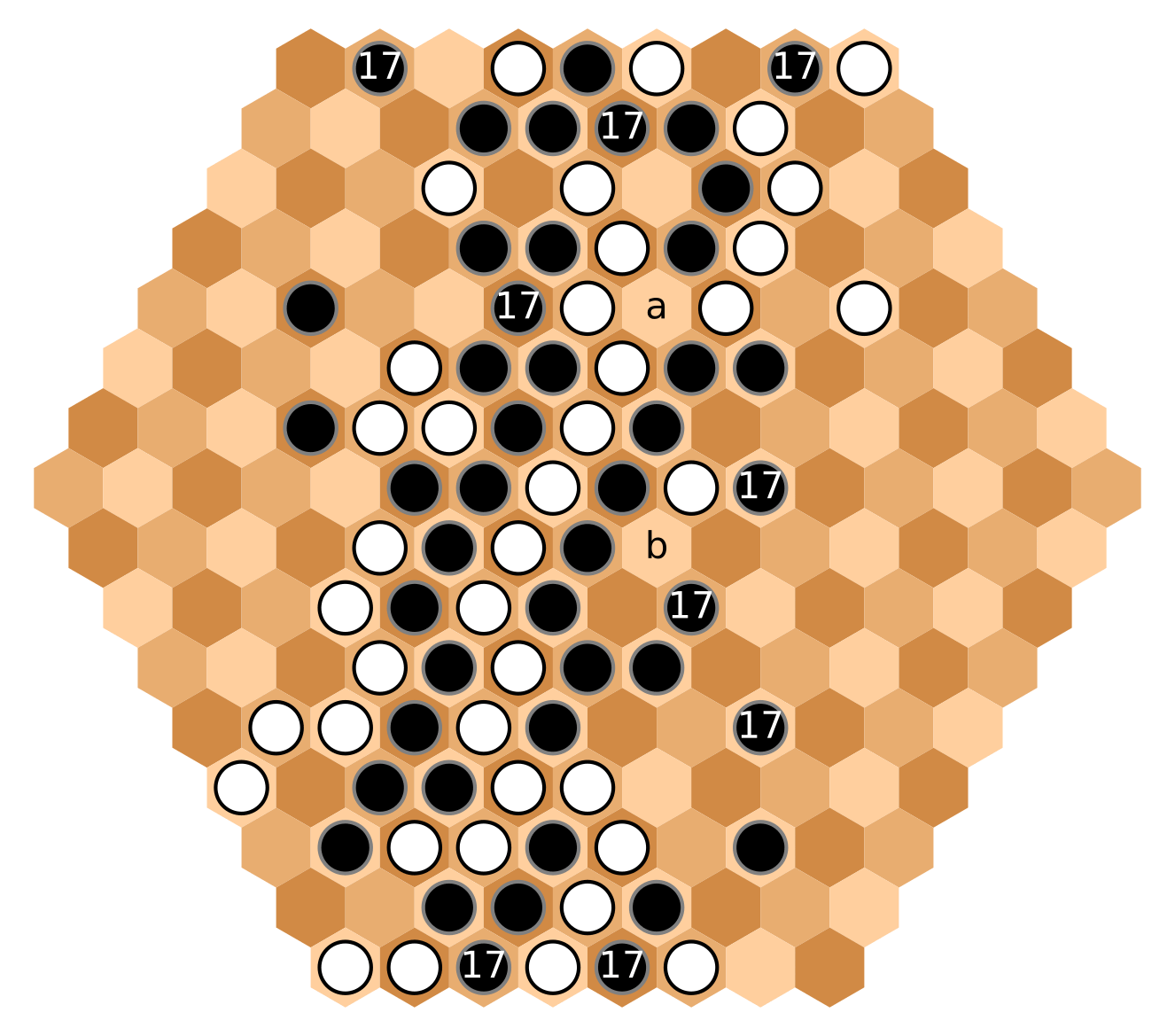
Black protects his three pieces, and expands to the north and east.
The hex [a] becomes decisive. Also, Black is threatening to win at [b].

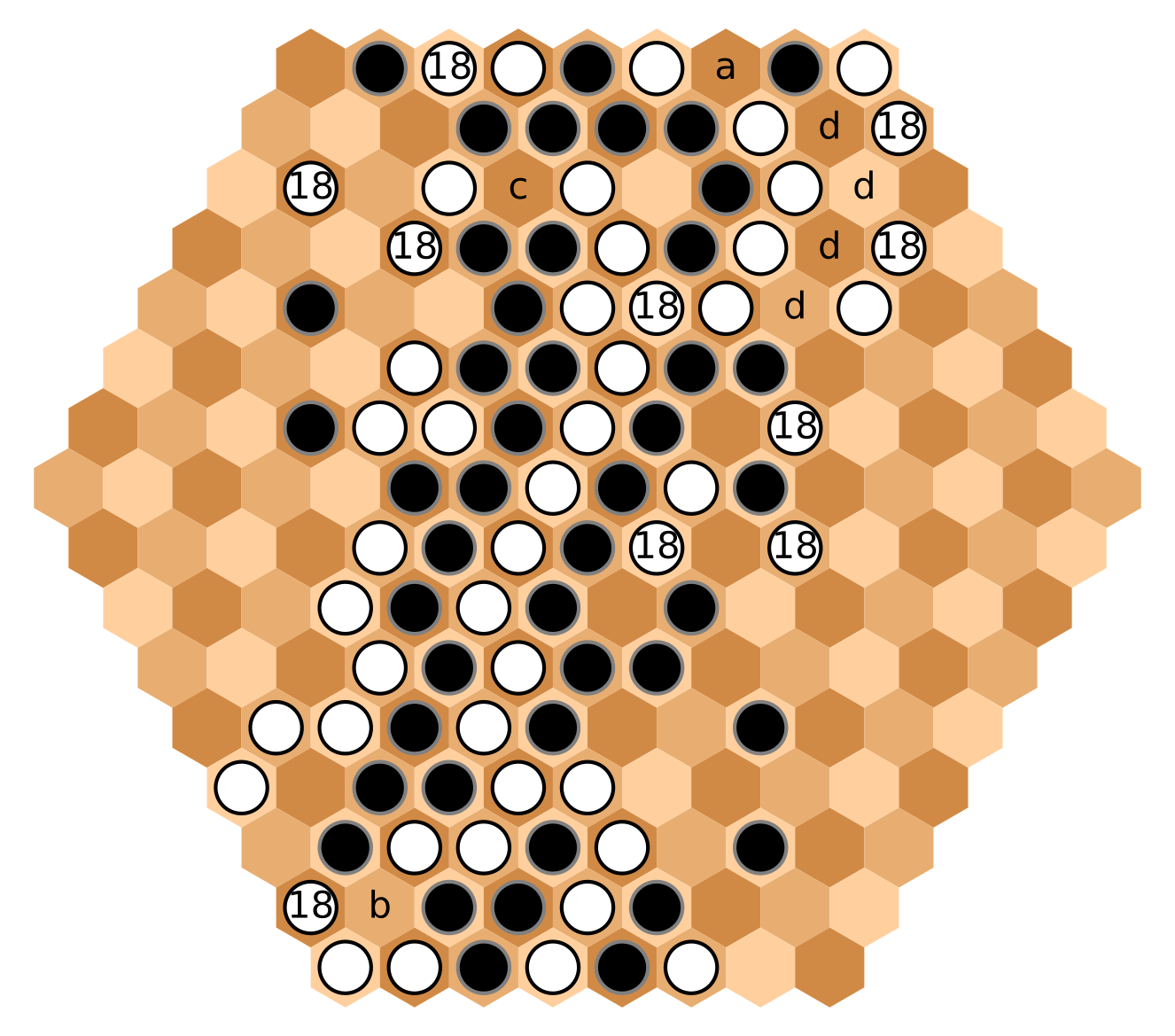
White now has 10 moves (!) She is able to develop an entire new branch at the east, while consolidating
her main group by playing at the previous hex [a], and still opening a new threat at the northeast.

In this position, Black resigns. He is forced to play at [a] and [b]. This opens White's [c], which
together with many options at [d], will connect three edge hexes in a winning pattern.

The final position: