Grafos - Caminho Mais Curto

O problema do caminho mais curto passa por encontrar, entre todos os caminhos possíveis entre dois nós de um grafo, aquele cujo custo é menor.

O custo de um caminho é a soma dos pesos das arestas que compõem esse caminho.

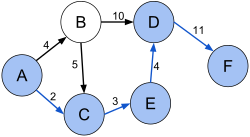
Por exemplo (ref):

O caminho mais curto entre A e F é dado pelos nós a azul, e o seu custo é dado por 2+3+4+11=20.

Existem dois caminhos alternativos, ABDF de custo 25, e ABCEDF de custo 27.

Algoritmo

Existem diversos algoritmos que permitem obter a solução.

O algoritmo que iremos implementar é a solução proposta por Dijkstra, sendo um algoritmo ganancioso (greedy algorithm).

Este algoritmo tem complexidade O( V² ) sendo V o número de nós.

Podem visualizar uma explicação do algoritmo neste tutorial:

O seguinte método implementa o algoritmo de Dijkstra usando as funcionalidades da classe Graph.

O método devolve null se não existir um caminho.

/**
 * Compute Shortest Path using Dijkstra's greedy algorithm
 * @complexity O(V^2)
 * @return an array with the indexes of the path, or null if no path exists
 */
public int[] shortestPath(int from, int to) {

   int[] costs = new int[size];
   for(int i=0; i<size ; i++)             // init costs
      costs[i] = Integer.MAX_VALUE-1;
   costs[from] = 0;

   boolean[] visited = new boolean[size];
   int visitedNodes = 0;

   int[] prev = new int[size];

   while(visitedNodes++ < size) {
      // select unvisited node with min cost
      int min = -1, minCost = Integer.MAX_VALUE;
      for(int i=0; i<size ; i++)
         if (!visited[i] && costs[i]<minCost) {
            min = i;
            minCost = costs[i];
         }

      if (minCost==Integer.MAX_VALUE-1) // no need to continue
         break;

      for(int succ : sucessors(min))
         if (minCost + weight(min,succ) < costs[succ]) {
            costs[succ] = minCost + weight(min,succ);
            prev[succ]  = min;
         }
      visited[min] = true;
   }

   // construct array with shortest path
   ArrayList<Integer> l = new ArrayList<Integer>();

   l.add(to);
   while(prev[l.get(0)] != from) {
      if (l.size() > size)      // something went wrong, no path is possible
         return null;
      l.add(0, prev[l.get(0)]); // add to begin of list, so the order is from --> to
   }
   l.add(0,from);
   return list2array(l);
}

Com este método podemos saber se dois nós estão conectados entre si:

/**
 * Is there a path from 'from' to 'to'? 
 * @complexity O(V^2)
 */
public boolean isConnected(int from, int to) {
   return shortestPath(from, to) != null;
}

Para experimentar tentem resolver o UVa 10514.

Tentem depois resolver alguns problemas desta lista que usam o algoritmo do caminho mais curto.