Geometria Computacional - Triângulos

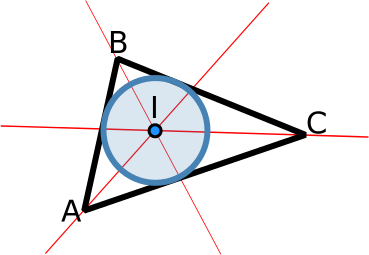
O triângulo é outra figura geométrica básica e que possui imensas aplicações.

Existem várias formas de especificar um triângulo. Definir os seus vértices, os seus ângulos ou, sem associação a coordenadas, definir a dimensão dos seus lados.

A classe seguinte opta por ter duas representações mutuamente exclusivas, uma definida pelos seus vértices e outra pela dimensão dos seus lados. Assim, consoante a informação disponível no problema, podemos construir um triângulo adequado. Para tal, haverá um atributo booleano que nos informa qual a representação de um dado objeto:

class Triangle {
  
  Point  A, B, C;   // defined by points
  double a, b, c;   // defined by sizes (no fixed reference) 
  boolean byPoints; // informs which representation we are using
  
  public Triangle(double a, double b, double c) {
    this.a=a; this.b=b; this.c=c; byPoints=false;
  }

  public Triangle(Point a, Point b, Point c) {
    this.A=a; this.B=b; this.C=c; byPoints=true;
  }
  
  public static double area(double a, double b, double c) { // Heron's formula
    double s = (a+b+c)/2.0;             // semi-perimeter
    return sqrt(s*(s-a)*(s-b)*(s-c));
  }

  // another method: https://www.futilitycloset.com/2018/09/07/neat-3/
  public static double area(Point p1, Point p2, Point p3) {
    return area(p1.distance(p2), p2.distance(p3), p3.distance(p1));
  }

  public double area() { return byPoints ? area(A,B,C) : area(a,b,c);  }

  public static double perimeter(Point p1, Point p2, Point p3) {
    return p1.distance(p2) + p2.distance(p3) + p3.distance(p1);
  }

  public double perimeter() {
    return byPoints ? perimeter(A,B,C) : a+b+c;
  }

O próximo método devolve o círculo inscrito num triângulo:

Este círculo pode ser descoberto pela intersecção de linhas que bisectam os ângulos do triângulo [ref]:

// returns the triangle's incircle
public Circle inCircle() {
    if (!byPoints) return null;
    
    Line angleBisector1 = Line.angleBisector(A, B, C),
         angleBisector2 = Line.angleBisector(B, A, C);
    
    Point center  = angleBisector1.intersect(angleBisector2);
    double radius = Triangle.area(A, B, C) / (0.5*Triangle.perimeter(A, B, C));
    return new Circle(center, radius);
}

Também podemos calcular o círculo que inscreve o triângulo.

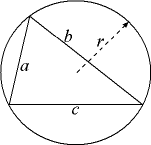
Este centro é a intersecção dos bisectores dos lados dos triângulos (o raio possui uma fórmula direta, cf aqui)

// returns the triangle's outcircle
public Circle outCircle() {
    if (!byPoints) return null;
    
    Line b1 = Line.bisector(A, B),
         b2 = Line.bisector(B, C);
    
    Point center  = b1.intersect(b2); 
    double radius = A.distance(B)*B.distance(C)*C.distance(A) / (4*Triangle.area(A, B, C));
    return new Circle(center, radius);
}

De notar que só podemos devolver estes círculos quando trabalhamos com a representação do triângulo por vértices.

Se tivermos só os lados, apenas podemos conhecer o raio destes círculos:

// returns the triangle's incircle radius (if we just know the sizes)
// @pre: !byPoints
public double radiusInCircle() {
    return Triangle.area(a, b, c) / (0.5*(a+b+c));
}

// returns the triangle's outcircle radius (if we just know the sizes)
// @pre: !byPoints
public double radiusOutCircle() {
    return a*b*c / (4*Triangle.area(a, b, c));
}

Outro método útil é saber quais os ângulos do triângulo. Se tivermos apenas os lados, os ângulos podem ser calculados pelas leis dos cosenos.

// return array of the triangle angles in radian
// to translate to degree use: 
//   Arrays.stream(t.angles()).map(rad -> rad*180.0/PI).toArray();
public double[] angles() {
    if (byPoints)
        return new double[] {Point.angle(C,A,B), Point.angle(A,B,C),Point.angle(B,C,A)};
    else {
        double a2=a*a, b2=b*b, c2=c*c; 
        return new double[] {acos((b2+c2-a2)/(2*b*c)),
                             acos((c2+a2-b2)/(2*a*c)),
                             acos((a2+b2-c2)/(2*a*b))};
    }
}

Uma nota sobre o método de cálculo da área. A fórmula de Heron é muito conhecida e matematicamente correta. Porém, no mundo dos double's esta fórmula levanta problemas de aproximação no caso de triângulos muito finos, onde dois lados são muito maiores que outro. Isto porque o semi-perímetro s vai ser muito similar aos dois lados maiores, e a subtracção de dois números muito similares pode levar a perda catastrófica de precisão (cf. o tutorial sobre este assunto).

Nesta situação, deve-se substituir por uma fórmula equivalente mais estável. A seguinte foi criada por William Kahan (devem respeitar os parenteses):

Problemas UVas sugeridos:

• UVa 00190 - Circle Through Three Points
• UVa 10195 - The Knights Of The Round Table
• UVa 10577 - Bounding box
• UVa 11152 - Colourful Flowers
• UVa 11909 - Soya Milk